ANGLE PROPERTIES OF A CIRCLE

Introduction

Arc, Chord and Segment

An arc is a part of the circumference of a circle. If an arc is less than half of the circumference, it is called a minor arc. If it is more than half, it is a major arc.

A chord is a line segment joining any two points on the circumference of a circle. The diameter is the longest chord in a circle.

A chord divides a circle into two parts. Each of these parts is called a segment. The smaller one is called the minor segment while the larger area is called the major segment. Note the difference between a segment and a sector. A sector is a part of the circle bound by an arc and two radii.

Throughout this article, you will see the word ‘subtends’ a lot. A subtended angle is the angle between two lines at a point.

In this diagram, AC subtends an angle $\theta$ at B.

In both of these diagrams, the arc AC subtends angle $\theta$ at B.

A circle is a very special shape, because lines and angles constructed in and around it have some very interesting properties. We will discuss some of these properties in this topic, and hopefully give you an appreciation for the elegance of geometry.

Angles at the Centre and at the Circumference

A chord or arc subtends an angle at the centre of a circle. It also subtends an angle at the circumference. However, there is something interesting about these angles. The angle subtended at the centre is twice the angle subtended at the circumference.

This is true for all angles that are subtended by the same chord or arc. The animation below shows how this relationship is maintained as the angle at the centre changes.

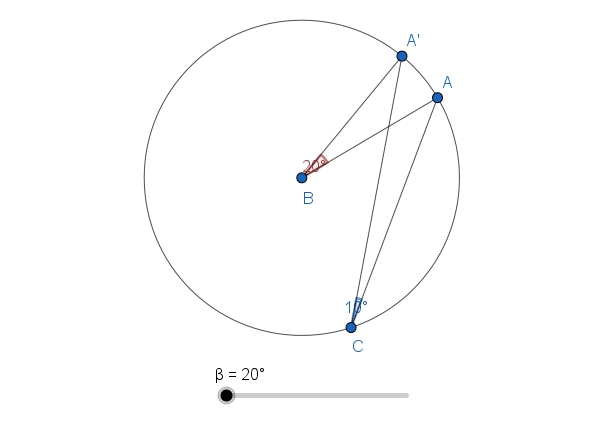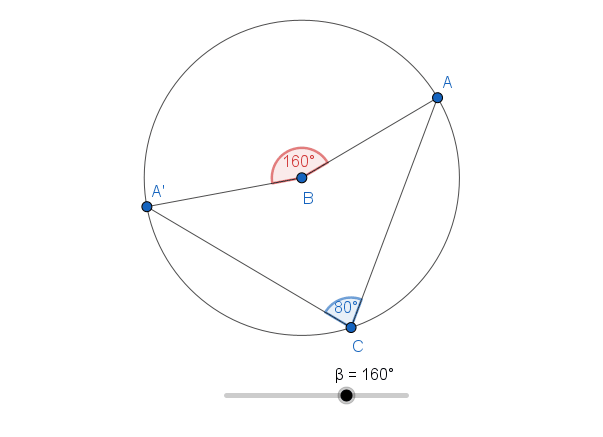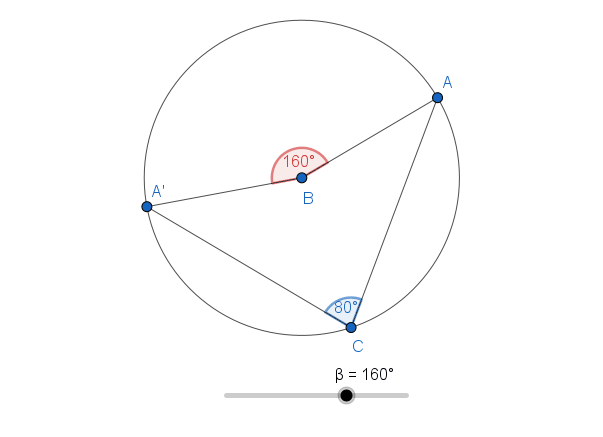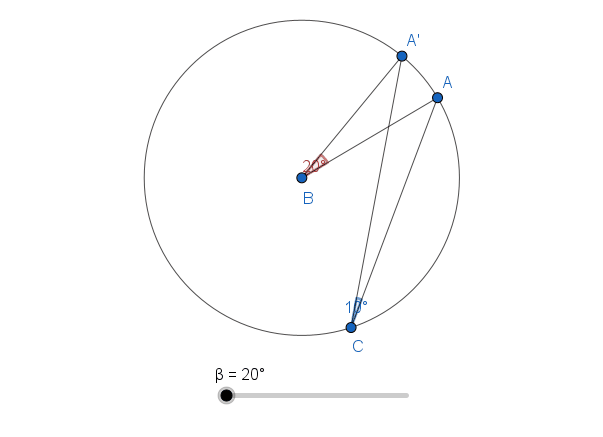
Click here to control the animation slider.

Why is this true?

Step	Diagram	Description
1		A, B, and D are points on the circumference and C is the centre of the circle. BC and CD are radii. AB and AD are chords.
2		Connect the points AC so that you have two triangles (ACD and ABC).
3		Let’s inspect triangle ACD.
4		We know that AC and CD are radii, so this is an isosceles triangle. The angles at A and D are therefore equal. We will label them $x$ .
5		As angles in a triangle add up to $180\degree$ , the angle at C will be 180 degrees minus the sum of the other two angles. This is expressed as $180-2x$ .
6		Now let us inspect triangle ABC.
7		BC and AC are radii so we have another isosceles triangle. The angles at A and B are equal. We will call them $y$ because this angle is not necessarily equal to $x$ .
8		Since angles in a triangle add up to $180\degree$ , the angle at C is $180-2y$ .
9		Now we have the diagram with all the angles filled in. We still need to prove that ∠BCD is equal to twice ∠DAB. First, let us simplify the angles within ADCB.
10		The angle at a is $x+y$ and the angle at C is the sum of $180-2x$ and $180-2y$ (or $180-2x+180-2y$ ). This simplifies to $360-2x-2y$ . Next, we need to find the angle on the other side of BCD.
11		We know that angles at a point add up to $360\degree$ . So, the obtuse angle BCD is: $360-(360-2x-2y)$ $=360-360+2x+2y$ $=2x+2y$ Thus, we have that the external angle BCD is $2x+2y$ . We can factor out 2 to get BCD as $2(x+y)$ .
12		$∠BAD=x+y$ and $∠BCD=2(x+y)$ , therefore $∠BCD=2∠BAD$ . Thus, the angle at the centre is twice the angle at the circumference.

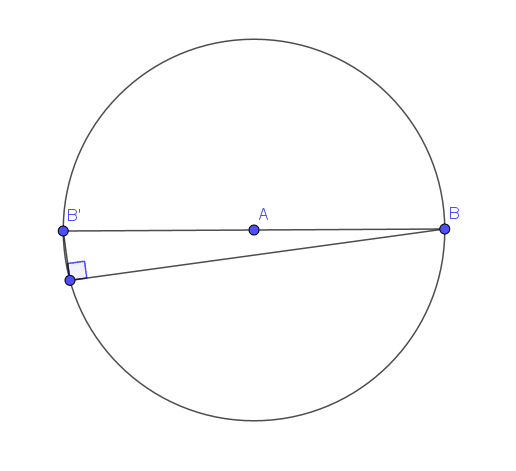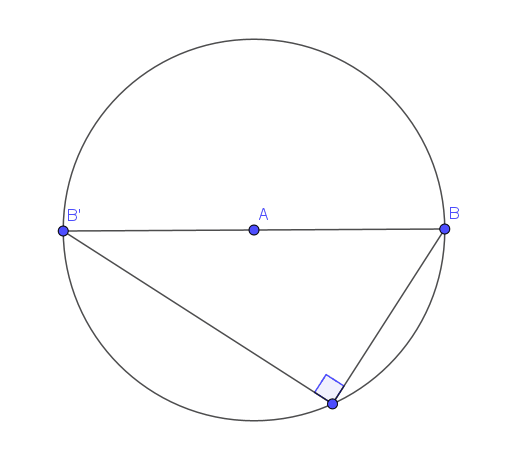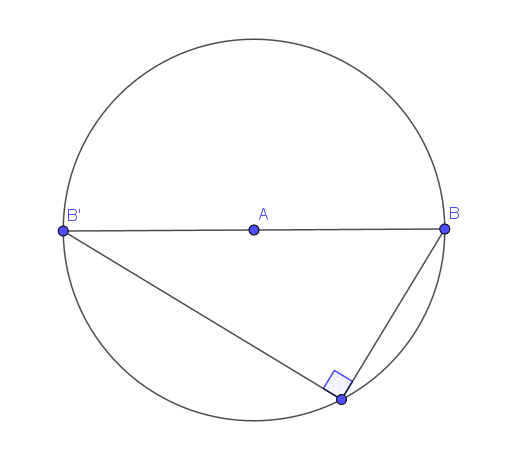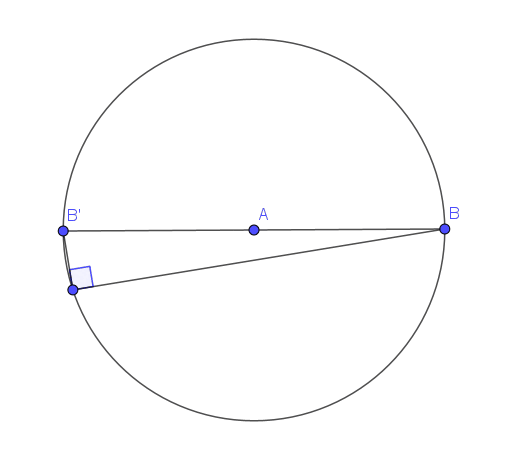
Think about how this property would apply to the diameter of a circle. It subtends 180 degrees at the centre, so at the circumference it must form half of this, or 90 degrees. When we look at the diagram, this is true!

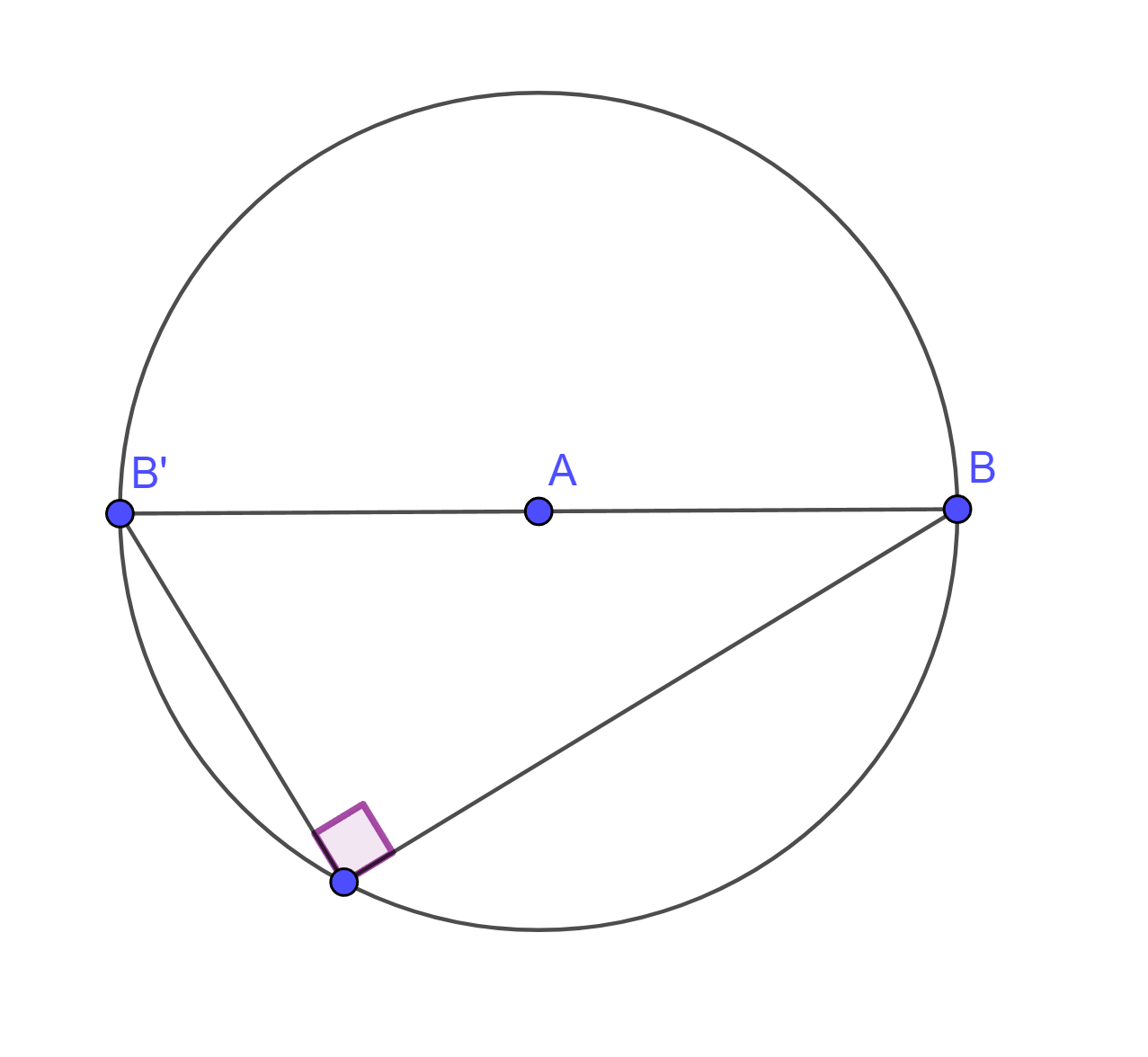
The angle subtended by a diameter is always 90 degrees. Observe that this angle stays the same even as the point moves around the circle.

Example 1

Find $\theta$ .

∠DAB = 180=39-104=37\degree

The angle at the centre is twice the angle at the circumference and so as we know the angle at the circumference ∠DAB, we need to multiply this by 2 to find θ.

∠BCD=37\times2=74\degree

Example 2

Calculate the size of $\theta$ .

AC and BC are both radii, so AC = BC.
ACB is therefore an isosceles triangle, so $∠CAB = ∠CBA = 46\degree$ .
The angle at the centre is twice the angle at the circumference and so as we know the angle at the circumference DAB, we need to multiply it by 2 to get the angle at the centre DCB.
$DCB=46\times 2$
$DCB= 92\degree$

Angles in the Same Segment

Angles subtended at the circumference by the same arc or chord in the same segment are equal.

In this diagram, DB divides the circle into two segments. DB subtends ∠DAB and ∠DCB at the circumference in the same segment. Therefore, these angles are equal as they are both subtended by the chord DB.

Equal arcs also subtend equal angles at the circumference.

Prove it!

To prove this, we will use the angle at the centre theorem that we covered earlier.

Diagram	Description
	We start by labelling the two angles at the circumference $a$ and $b$ .
	Draw two radii from the centre to the circumference (here these are dashed lines). Label the angle between the two radii $c$ .
	We will first look at the angles $a$ and $c$ .
	We know that the angle at the centre is twice the angle at the circumference. This means that if the angle at the centre is equal to $2x$ , then the angle at the circumference is $x$ .
	Let us now examine angles $b$ and $c$ .
	We know that the angle at the centre is twice the angle at the circumference. Since the angle at the centre is $2x$ , the angle $b$ is equal to $x$ .
	We now have that $a$ and $b$ are equal to $x$ . Thus, the two angles are equal. We can therefore conclude that angles subtended by the same arc in the same segment are equal.

Example

Find ∠ABD.

$∠AOD=360-306=54\degree$ (Angles at a point)
$∠ACD=54\div2=27\degree$ (Angle at the centre is twice the angle at the circumference)
$∠ABD=∠ACD=27\degree$ (Angles in the same segment are equal)

Cyclic Quadrilaterals

A cyclic quadrilateral is a quadrilateral whose vertices all lie on the circumference of a circle. The vertices are called concyclic points because they all lie on the same circle.

Here, ABCD is a cyclic quadrilateral. The points A, B, C and D are concyclic.

Opposite Angles of a Cyclic Quadrilateral

The opposite angles of a cyclic quadrilateral are supplementary (add up to 180 degrees). This is true for all cyclic quadrilaterals.

Proof

Diagram	Description
	ABCD is a quadrilateral inscribed by a circle with centre O.
	By drawing two radii from OB and OD, we can split the quadrilateral into two smaller quadrilaterals, ADOB and DOBC.
	If the angle A is labelled $a$ , the angle BOD is equal to $2a$ as the angle at the centre is twice the angle at the circumference.
	If the angle at C is labelled $c$ , the other angle at BOD is equal to $2c$ for the same reason as in Step 3.
	This means that we have the point at the centre with the angles 2a and 2c. Since angles at a point add up to 360 degrees, $2a+2c=360\degree$ Dividing this by 2, we get $a+c=180\degree$ Therefore, opposite angles of a cyclic quadrilateral add up to 180 degrees.

Exterior Angles of a Cyclic Quadrilateral

We’re going to start by stating this property of cyclic quadrilaterals, then we will break it down. It is that if a side of a cyclic quadrilateral is produced, the exterior angle formed is equal to the interior opposite angle.

In other words, when a side of a cyclic quadrilateral is extended, the exterior angle formed is equal to the angle that is opposite the interior angle. Let us see why this is true.

Proof

To prove:

∠BCE = ∠DAB

∠DCB + ∠BCE = 180\degree\qquad \text{(Angles on a straight line add up to 180\degree)}

∠DCB+∠DAB=180\degree\qquad\text{(Opposite angles of a cyclic quadrilateral)}

Equating the above cases, we get:

∠DCB + ∠BCE=∠DCB+∠DAB

∠BCE=∠DAB

Example 1

Calculate angle ADC.

Solving problems in math is often just wishful thinking. In this case, it would be great if we had ∠ABC so we could simply subtract it from 180 to get $\theta$ . But how can we find a way to do this?

We see that OB and OC are equal, so OBC is an isosceles triangle. Thus, we can calculate ∠OBC. $∠OBC=(180-100)\div2=40\degree$ Now, we add ∠ABO and ∠OBC. $48+40=88\degree$ Now we have the angle that we wanted! As opposite angles of a cyclic quadrilateral total 180 degrees, we can calculate the size of angle ADC. $∠ADC=180-88=92\degree$

Example 2

VWZ is a straight line. Calculate the size of angle ZXY.

The exterior angle VWX is equal to the interior opposite angle XYZ.
$∠VW \! X=∠XY \! Z=97\degree$

We can now find ZXY using the property that angles in a triangle add up to 180 degrees. $∠ZXY=180-(97+43)=40\degree$

Note that it is important to look at all the possible ways of solving a problem before tackling it. The best solution is not always the most obvious, so make sure to look for it.

Summary

The angle subtended by an arc or chord at the centre of a circle is twice the angle subtended at the circumference.

The angle subtended at the circumference by a diameter is 90 degrees.

Angles subtended at the circumference by the same arc or chord in the same segment are equal.

Opposite angles of a cyclic quadrilateral are supplementary.

If a side of a cyclic quadrilateral is produced, the exterior angle formed is equal to the interior opposite angle.

Credit to Third Space Learning for some of the diagrams and proofs used in this article. For more resources, visit https://thirdspacelearning.com/gcse-maths/geometry-and-measure/

ANGLE PROPERTIES OF A CIRCLE

Introduction

Arc, Chord and Segment

Angles at the Centre and at the Circumference

Example 1

Find \theta.

Example 2

Calculate the size of \theta.

Angles in the Same Segment

Example

Find ∠ABD.

Cyclic Quadrilaterals

Opposite Angles of a Cyclic Quadrilateral

Exterior Angles of a Cyclic Quadrilateral

Example 1

Calculate angle ADC.

Example 2

VWZ is a straight line. Calculate the size of angle ZXY.

Summary

Find $\theta$ .

Calculate the size of $\theta$ .