POLYGONS

A polygon is a shape with straight sides that do not cross each other. There are two types of polygons:

Regular polygons – Polygons with equal sides and equal angles.
Irregular polygons – Polygons with sides of different lengths and angles of different sizes.

The following are some examples of regular and irregular polygons.

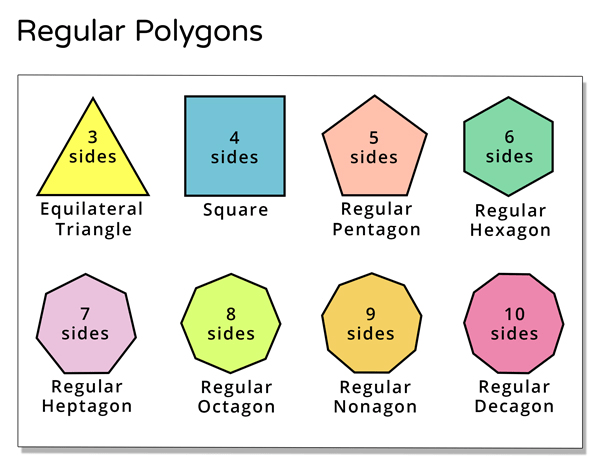
The sum of interior angles for any polygon is given by the formula $\text{Sum of interior angles} = (n-2)\times180\degree$ where $n$ represents the number of sides.

Why does this formula work?

The proof of this formula involves dividing the given polygon into a number of triangles from a common point. Let us demonstrate this using a pentagon:

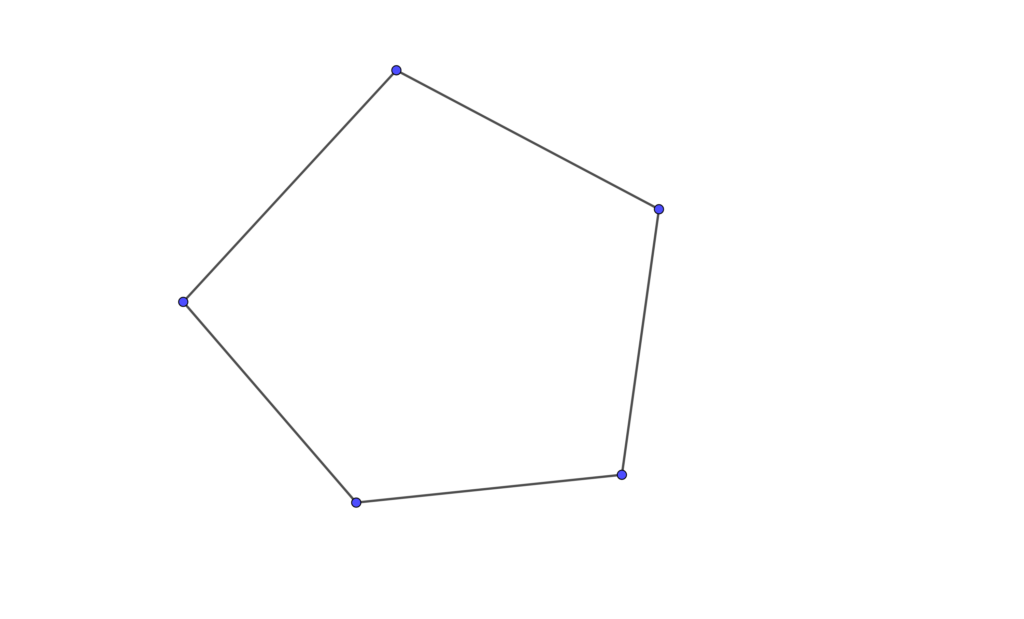We can divide this shape into 3 triangles by drawing lines from one vertex to all the other vertices:

We know that the sum of the interior angles of a triangle is $180\degree$ . Since there are 3 triangles in this shape, the total is: $\text{Sum of interior angles} = 3\times180 = 540\degree$

And there we have it! The sum of the interior angles of a pentagon is $540\degree$ .

You could apply this method to find the sum of interior angles of polygons with more sides. However, we can come up with a simple formula that makes this much easier.

Consider a polygon with $n$ sides. Drawing lines from one vertex to all the other vertices gives $n-2$ triangles (see for yourself that the number of triangles is always 2 less than the number of sides by testing with different polygons). So, the sum of interior angles for a polygon with $n$ sides is the number of triangles times $180\degree$ .

\begin{align*} \text{Sum of interior angles} &= (n-2) \times 180\degree \\[5pt] &=180\degree(n-2) \end{align*}

The sum of exterior angles of any polygon is $360\degree$ . This is a useful fact that will be applied in many areas later in this article.

Proof

We want to prove that the sum of exterior angles of any polygon is $360\degree$ . We know that $\text{Exterior angle} + \text{Interior angle} = 180\degree$ .

If a polygon has $n$ sides, then there are $n$ exterior angles and $n$ interior angles. Thus, we can multiply both sides of the above equation by $n$ to get the sum of all exterior and interior angles. $n(\text{Exterior angle + Interior angle})=180\degree\times n$ $\text{Sum of exterior angles }+ \text{ Sum of interior angles }=180\degree \times n$

The sum of exterior angles is therefore: $\text{Sum of exterior angles }=(180\degree \times n) -\text{ Sum of interior angles}$

Earlier, we found that the sum of interior angles is equal to $180\degree(n-2)$ . Substituting this into our equation: $\text{Sum of exterior angles }=(180\degree \times n) -180\degree(n-2)$

Opening the brackets and simplifying, we get: $\text{Sum of exterior angles }=180n -180n+360$ $\boxed{ \text{Sum of exterior angles }=360\degree}$

Regular Polygons

In regular polygons, the size of each angle is equal. Therefore, we can determine the size of each angle by dividing the sum of the interior angles by the number of sides: $\text{Size of interior angle} = \frac{180\degree(n-2)}{n}$

Similarly, the size of one exterior angle can be found by dividing $360\degree$ (the sum of exterior angles) by the number of sides in the polygon: $\text{Exterior angle}=\frac{360\degree}{n}$

We can divide both sides of this formula by the size of exterior angle and multiply both sides by $n$ to get another useful formula: $n=\frac{360\degree}{\text{Size of exterior angle}}$

Polygons have a variety of applications in the real world. For example, they are fundamental in architecture and construction, used in designing buildings, bridges and other structures. Polygons are also extensively used in computer graphics and animation to represent 3D objects and create models of characters, environments and special effects.

Example 1

Two interior angles of an irregular polygon each measure $90\degree$ . All the other remaining interior angles each measure $150\degree$ . Determine the number of sides of the polygon.

We know that the sum of interior angles of any polygon is equal to $180\degree(n-2)$ . If we can find a way to equate the sum of interior angles of our polygon to this general formula, we might be able to find the answer. In this problem, we are given the size of two angles as $90\degree$ , and the rest are $150\degree$ . To find the sum of interior angles in this polygon, we need to know how many angles are $150\degree$ . But how can we do this?

Since we don’t know the number of sides of our polygon, we can let the number of sides be $n$ . Since 2 angles are $90\degree$ , then $n-2$ angles are $150\degree$ .

We can now equate the sum of interior angles of the polygon in the question to the general formula: $\text{Sum of interior angles} = 180\degree(n-2)$ $\text{Sum of interior angles} = 2\times90\degree+(n-2)\times150\degree$ $2\times90\degree+(n-2)\times150\degree= 180\degree(n-2)$ $180+150n-300=180n-360$ Simplifying the equation, we obtain: $30n=240$ $\boxed{ n=8 }$

Example 2

The sum of interior angles of a regular polygon is $1800\degree$ . Find the size of each exterior angle.

The size of an exterior angle is equal to $\dfrac{360\degree}{n}$ , where $n$ is the number of sides. Thus, we need to find the number of sides in order to find the size of an exterior angle. What information do we have that can help us find the number of sides?

The sum of interior angles of a polygon is given by the expression $180\degree(n-2)$ . We know that the sum is equal to $1800\degree$ , so we can equate the two: $180(n-2)=1800$ $180n-360=1800$ $180n=2160$ $n=12$ We can now use this to find the size of an exterior angle. $\begin{align*} \text{Exterior angle}&=\frac{360\degree}{n} \\[8pt]&=\frac{360}{12}\\[8pt]&=\boxed{30\degree}\end{align*}$

Example 3

The size of an interior angle of a polygon is 6.5 times that of its exterior angle. Determine the number of sides of the polygon.

We know that: $n=\frac{360\degree}{\text{Size of exterior angle}}$

Thus, to find the number of sides of the polygon, we need to find the size of each exterior angle. Let the size of an exterior angle be $x$ . The interior angle is 6.5 times larger than this, or $6.5x$ . We can use the fact that the sum of an exterior and interior angle is equal to $180\degree$ to find $x$ .

$\text{Exterior angle + Interior angle} = 180\degree$ $x+6.5x=180\degree$ $7.5x=180\degree$ $x=24\degree$ Now that we have the exterior angle, we can find the number of sides. $\begin{align*} n&=\frac{360\degree}{\text{Size of exterior angle}}\\[11pt] &=\frac{360\degree}{24\degree}\\[9pt]&=\boxed{15\text{ sides}} \end{align*}$

Example 4

The sum of interior angles of a regular polygon is 24 times the size of the exterior angle. Find the number of sides of the polygon.

NOTE: This is a Form 2 level question. If you are in Form 1, do not worry about not understanding some of the final steps.

Our goal here is to find the number of sides, $n$ , of the polygon. Thus, we need to find a way to form an equation in $n$ . Let us start by writing down what we know, and maybe that will relate us to $n$ .

$\text{Sum of interior angles} = 180\degree(n-2)=180n-360$ $\text{Exterior angle}=\frac{360\degree}{n}$

From the question: $\text{Sum of interior angles} = 24(\text{Exterior angle})$

We can substitute the expressions for sum of interior angles and for size of an exterior angle into our equation. $180n-360=24\left(\frac{360\degree}{n}\right)$ $180n-360=\frac{8640\degree}{n}$ To simplify further, we can multiply both sides of the equation by $n$ in order to remove the denominator on the right side of the equation. $180n^2-360n=8640$ $180n^2-360n-8640=0$

Now, this looks oddly familiar. It is a quadratic equation, which we know how to solve! We can divide both sides of the equation by 180 to simplify. $n^2-2n-48=0$ $n^2-8n+6n-48=0$ $n(n-8)+6(n-8)=0$ $(n+6)(n-8)=0$ $n=-6\text{ or }8$ $\text{The number of sides cannot be negative, therefore:}$ $\boxed{n=8}$