Vectors (I)
Introduction
A vector is a quantity that has both magnitude (size) and direction. Vectors can be interpreted as displacement from a point. Think of it as how to move from point A to point B. You would have to move in a certain direction, and a specific distance to get to the desired location.
The direction of a vector is shown by an arrow.
A vector AB can be represented in 3 ways: \utilde{AB} , \vec{AB} or AB (in bold). In print, bold is normally used (AB), but in writing we use the wavy line beneath the vector to represent it \left( \utilde{AB} \right) .
Sometimes, a vector may be represented by a single letter e.g. \utilde{a} , a
Vectors are written in the form \dbinom{x}{y} , where x is the displacement in the x-axis while y is the displacement in the y-axis. For example, \dbinom{5}{2} means a displacement of 5 units in the x direction and 2 units in the y direction.
Addition of Vectors
Consider a displacement from A to B, then from B to C.
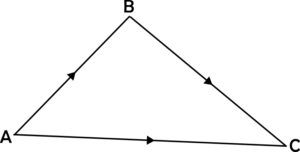
The resulting displacement is AC. This is written as AB + BC = AC.
In addition of vectors, \utilde{a}+\utilde{b}=\utilde{b}+\utilde{a} . This is because 2 displacements in any order ultimately get to the same point.
In this example, both \utilde{a}+\utilde{b} and \utilde{b}+\utilde{a} get you from point X to point Y. This applies to all cases.
When adding vectors, we add the x components and the y components separately. e.g. \dbinom{5}{-2}+\dbinom{6}{1}=\dbinom{5+6}{-2+1}=\dbinom{11}{-1}
Multiplication of a Vector by a Scalar
Multiplication of a vector by a scalar quantity is similar to normal multiplication. Each component of the vector is multiplied by the scalar to give the answer. For example:
If a = \dbinom{3}{2} and b = \dbinom{1}{4} , find 3a + 2b.
\begin{split}3\bold{a}+2\bold{b}&=3\dbinom{3}{2}+2\dbinom{1}{4} \\ &=\dbinom{9}{6}+\dbinom{2}{8} \\ &=\dbinom{11}{14}\end{split}Position and Column Vectors
A position vector is a vector that starts from the origin to a point.
A column vector is one that starts from a point and ends at another point.
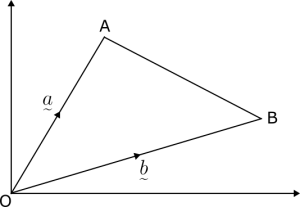
In this example, OA and OB are position vectors, while AB is a column vector.
Let us see how we can represent AB in terms of \utilde{a} and \utilde{b} . AB can be represented as:
AB = AO + OB.
However, AO is moving in the opposite direction as OA, thus we need to use a negative sign to represent it.
AO = – OA
AO = – \utilde{a}
OB is equal to \utilde{b} . Putting this all together:
AB = AO + OB
AB = – \utilde{a} + \utilde{b}
From this, we see that when going in the opposite direction of a vector, we negate it.
Generally, position vectors are notated using the letters i and j. For example, the vector \dbinom{3}{4} can be represented as 3i + 4j.
The letters i and j are called unit vectors. i is the unit vector for the x direction, while j is the unit vector for the y direction.
The term ‘unit vector’ means the vector that represents a movement of one unit in the axis that it represents. For example, i is the vector \dbinom{1}{0} , as it represents a movement of one unit in the x direction. Similarly, j is the vector \dbinom{0}{1} , representing a displacement of 1 unit in the y direction.
An expression such as 2i + 6j means to multiply the scalar by the unit vector. \begin{split}2\bold{i}+6\bold{j}&=2\binom{1}{0}+6\binom{0}{1}\\&= \binom{2}{0}+\binom{0}{6}\\&= \binom{2}{6}\end{split} Generally, you don’t need to go through the steps of multiplying like this. Just take the coefficients (i.e. 2 and 6) as the x and y displacements.
In 3 dimensional vectors, the letter k is used to represent a movement in the z direction. This will be covered in Form 3.
Midpoint and Magnitude
The midpoint of a vector is the point at the centre of the vector.
Given two sets of coordinates, the midpoint is calculated as: \left( \frac{x_1+x_2}{2},\frac{y_1+y_2}{2} \right)
The modulus/magnitude/length of a vector means how long the vector is. It does not have a direction. It is represented using two vertical bars on either side of the vector, |AB| .
Modulus is calculated as: \sqrt{ \left( x_2-x_1 \right)^2+ \left( y_2-y_1 \right)^2}
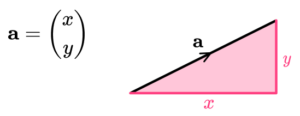
Generally, if a = \dbinom{x}{y} , the magnitude of the vector is given by: \sqrt{x^2+y^2}
If this formula seems familiar, that’s because it is the same formula as the Pythagorean theorem. In our case, the vector is the hypotenuse, while the x displacement is the base of the triangle and the y displacement is the height.
Note: Always remember that vectors have direction. AB is NOT the same as BA. Think of it as moving from the first point to the second point, following a certain path. This is why negating is so important, even though it is often overlooked.
Example 1
The coordinates of points A and B are A(3, 4) and B(11, 2).
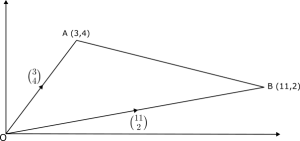
(a) Find the coordinates for the midpoint of AB.
\begin{split}\text{Midpoint}&=\left( \frac{x_1+x_2}{2},\frac{y_1+y_2}{2} \right)\\&=\left( \frac{3+11}{2},\frac{4+2}{2} \right)\\&= \left( \frac{14}{2},\frac{6}{2} \right)\\&=(7,3)\end{split}(b) Find the modulus of AB.
\begin{split}\bold{AB}&=\bold{AO}+\bold{OB}\\&=-\binom{3}{4}+\binom{11}{2}\\&=\binom{-3}{-4}+\binom{11}{2}\\&=\binom{8}{-2}\end{split} \begin{split}|\bold{AB}|&=\sqrt{x^2+y^2}\\&=\sqrt{8^2+(-2)^2}\\&=\sqrt{68}\\&=8.246\end{split}Example 2
Vector OP = 6i + j and OQ = -2i + 5j. A point N divides PQ internally in the ratio 3 : 1. Find PN in terms of i and j.
To get PN, we must move from P to O then O to N i.e. PN = PO + ON.
Thus, we can start by finding ON. \begin{split}\utilde{ON} &= \utilde{OP} +\frac{3}{4}\ \utilde{PQ}\\&=\utilde{OP}+\frac{3}{4} \left( \utilde{PO}+\utilde{OQ} \right)\\&=\binom{6}{1}+\frac{3}{4}\left[\binom{-6}{-1}+\binom{-2}{5}\right] \\&=\binom{6}{1}+\frac{3}{4}\binom{-8}{4}\\&=\binom{6}{1}+\binom{-6}{3}\\&=\binom{0}{4}\end{split}
Now that we have ON, we can plug it into the original equation to find PN. \begin{split}\utilde{PN}&=\utilde{PO}+\utilde{ON}\\&=\binom{-6}{-1}+\binom{0}{4}\\&=\binom{-6}{3}\end{split} Finally, expressing in terms of i and j:
PN = -6i + 3j
Example 3
In the figure below, AB = p, AC = q, AD = \frac{3}{5} AC and CE = \frac{2}{3} CB. Express DE in terms of p and q.
\begin{split} DE &= DC + CE\\ &=\frac{2}{5}AC+\frac{2}{3}CB \end{split} DE=\frac{2}{5}\ \utilde{q}+\frac{2}{3}(CA+AB) DE=\frac{2}{5}\ \utilde{q}+\frac{2}{3} \left( -\utilde{q}+\utilde{p} \right) DE=\frac{2}{5}\ \utilde{q}-\frac{2}{3}\ \utilde{q}+\frac{2}{3}\ \utilde{p} \boxed{\utilde{DE}=\frac{2}{3}\ \utilde{p}-\frac{4}{15}\ \utilde{q}}
Translation
Translation is the movement of a point or line in a certain direction. The length and orientation of the line do not change, only its position.
A good mnemonic for calculation of translations is TOI : \text{Translation vector + Object = Image}
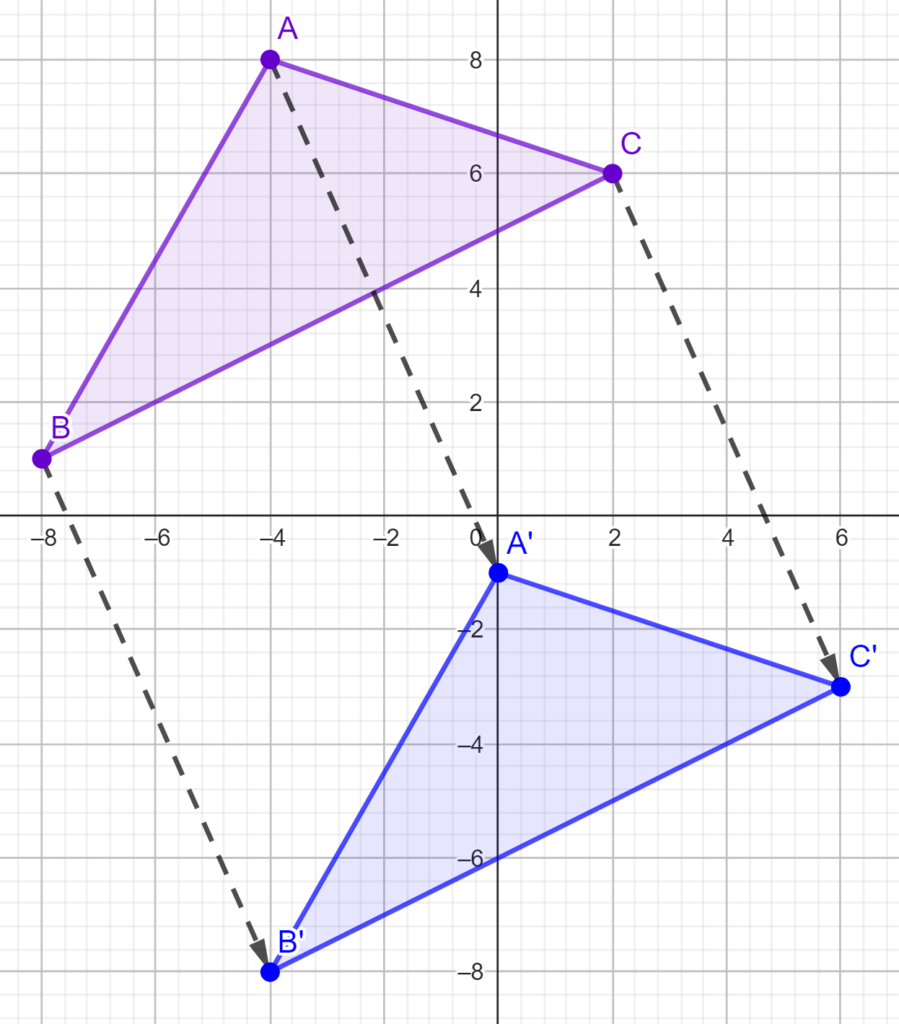
In the diagram above, triangle ABC undergoes a translation \binom{4}{-9}. Note that each point moves through the same vector and the shape has the same size and orientation. It is just shifted downwards and to the right. Let us now examine a word problem.
Example
Two points P and Q have coordinates (-2, 3) and (1, 3) respectively. A translation maps point P to P'(10, 10). Find the coordinates of Q’, the image of Q under the same translation.
First, we need to find the translation vector. This is given by the coordinates of the image P’ minus those of the object P. T= \binom{10}{10}-\binom{-2}{3}=\binom{12}{7} Now, applying this translation to Q (1, 3): Q'=\binom{12}{7}+\binom{1}{3}=\binom{13}{10} Note that the answer cannot be left as a vector, it has to be written as coordinates. Thus, our final answer is Q'(13, 10).
It may also be helpful to draw a sketch of what the question represents in order to help you understand it. We encourage you to draw a diagram for this problem.
Vectors are applied in various fields such as science and engineering. They are used in navigation to represent position, velocity and direction. They are used in meteorology to represent wind speed and direction, which are crucial for weather forecasting. Even in video games, vectors come to play in the simulation of realistic movement and interactions. These are just a few examples, the applications of vectors are vast and diverse, playing a fundamental role in numerous scientific and technological fields.